Tom Lubensky

Zierler:

Okay. This is David Zierler, oral historian for the American Institute of Physics. It’s my great pleasure to be here with Professor Tom Lubensky on May 4, 2020. Tom, thank you so much for being with me today.

Lubensky:

My pleasure.

Zierler:

Okay. So to start, would you please tell me your title and institutional affiliation?

Lubensky:

Okay. I am a Christopher H. Browne Distinguished Professor Emeritus.

Zierler:

So to really put you on the spot, who was Christopher H. Browne, or who is Christopher H. Browne?

Lubensky:

You know, I’m not absolutely positive. He’s endowed a number of chairs at Penn, including the president, who holds a chair of the same name. He is a Penn alumn, graduating in 1969 with a B.A. in history. He became an investment broker focusing on value investing. He did quite well. He donated $25 million to establish several endowed professorships at Penn, where he was a trustee.

Zierler:

Oh, really? Not just physics.

Lubensky:

No, not just physics. This is a university… Well, an SAS-wide one. I’m not sure… No, I guess it’s university-wide probably, but I’m not positive.

Zierler:

Okay. Well, I’ll bring you right back to areas you're going to know a lot more about than him. Let’s start right with your beginnings. Tell me about your birthplace and your family and your early childhood.

Lubensky:

Okay. This gets to be a long story. It’s different from most.

Zierler:

Okay!

Lubensky:

So my heritage is western Missouri. I was born in Kansas City in ’43 in the midst of the war when my father was in Fairbanks, Alaska. My mother grew up on a dirt-poor farm with no running water, no electricity, an outhouse, and all of that. Her mother died early and she was raised by her grandmother, who was born before the Civil War. My father’s side, you know, even though the name is Lubensky… We do have ancestors named Lubensky, but they mostly died coming over to Texas in the 1850s.

Zierler:

Is that a Polish name, Lubensky?

Lubensky:

It’s a Polish name, and Poles will recognize it. So the town of origin is Breslau in German Silesia in the 19th century, but now the city of Wroclaw in Poland. On that line, we haven't gone back too far. On my mother’s side, you know, she is a direct descendant of the Prices who came to Virginia in 1610 or something like that.

Zierler:

Wow.

Lubensky:

First decade and a half of the 17th century. We can trace the line all the way back to there, and the claim is there are some Welsh ancestors that might have been nobility. Who knows? So that’s on one side. On my grandmother’s side (my father’s mother’s side), it’s pure Catholic German. She was educated in German, in fact, in Missouri. She was born in 1895 and so it was in the early 1900’s that she was a student, and the language of instruction was German using textbooks published in Cincinnati, actually. So I’m part of that substantial German community in Missouri along the Missouri River valley.

Zierler:

Now you mentioned your father was in Alaska at some point?

Lubensky:

Yeah, he was drafted in the war and he was in Alaska at that time during the war in ’43.

Zierler:

What was he doing there?

Lubensky:

Well, there he was mostly a buck private, you know, protecting Alaska. He didn't see any combat, but he was sent back… He was drafted, so he went in as a buck private. He took a bunch of tests and they decided he was officer material, and so he was sent to OCS. He eventually ended up being one of the people in charge of a German prisoner-of-war camp in Charleston, South Carolina, where my middle brother was born (I have a younger brother who now lives in Ecuador – another story). I should say that my father’s family were basically small businessmen. They had grocery stores during the Depression, he and my father’s father and his brother. My father’s father died when my father was 16. My father had actually entered premed school at the Missouri Valley College in Marshall, Missouri, where he was born, to follow the footsteps of one of his grandfathers who actually had a kind of degree or certificate from NYU, I think it was, in medicine. But the depression sort of devastated them. They lost essentially everything. They still retained the house in Marshall, Missouri where I do remember some aspects of it.

But while my father was in the Army, he decided he wanted to do good things for the world, so he gave himself two choices. He was either going to pass the Foreign Service exam and become a diplomat, or he was going to homestead land in Alaska, and he wasn’t sure which one. So after my father completed his degree under the GI Bill at Missouri Valley College, which is I think known only for wrestling championships in western Missouri [chuckles], we went to Washington. My father went for two years to Georgetown and obtained a degree from is School of Foreign Service—

Zierler:

Yeah.

Lubensky:

—working at the Library of Congress and selling real estate to pay for three kids. My mother, of course, never went to college. I’m not the usual cut from the physics “cookie cutter.”

Zierler:

Yeah. So how old were you during the Washington years?

Lubensky:

Oh, so Washington… We left Missouri in ’47, so I was four, and then we left to Germany in March 1950 when I was six. So I went to the first semester of first grade in a little town called Radiant Valley, Maryland which is one of the many postwar housing developments.

Zierler:

Mm-hmm [yes]. Your father was serving in the embassy in Germany?

Lubensky:

Well, at that time, he… Well, no. So he was part of the re-democratization program. We sent diplomats… They were sort of at that time, not officially part of the Foreign Service, the Diplomatic Corps. They were treated as diplomats, but they were really designated to teach Germans how to go back to democracy.

Zierler:

He was a State Department employee or no?

Lubensky:

Yeah, yeah. He was in the State Department, and eventually while he was in Germany he was “promoted” to full-fledged membership of the Diplomatic Corps … Had to take a cut in salary to do that, but… [Chuckles] So we lived in Frankfurt for a month or so, and then we were in a place called Kassel, fairly near the East German border, for, I think, four months. Then finally we went to a little town called Fritzlar. So my father was what they called a Kreis Resident Officer. He was in charge of the Amerika Haus there and the re-democratization procedures. So there were no Americans there, but there was a US military base nearby, and I was able to go to an American School run by the Army. It was right at the boundary between the French and American zones, so my youngest brother went to a French nursery school.

Zierler:

So re-democratization, is that a nice way of saying de-Nazification or not necessarily?

Lubensky:

Well, I’ve never heard that term used. We called it re-democratization. So it was basically, you know, get to know the leaders of the town, the mayor and so forth, and encourage them to develop democratic norms. I had one very good German friend who was older than I was. He sort of appeared at our doorstep one day, so I kicked around with him, as did my brothers. I was fluent in German when I was seven, but when I left and went back to the States to see my grandmother who insisted I speak some German to her, I refused to do it. But my accent is such that people can get fooled a little bit there.

Zierler:

So you’ve kept up your German.

Lubensky:

No, not so much. I mean I can speak it a little bit, but I have a vocabulary of a seven-year-old at this point.

Zierler:

Just to fast forward, did you ever draw on your German for your career in physics?

Lubensky:

You know, no. No. I drew on it to… You know, my wife and I in 1970 drove from Paris to Ankara and back, and there, in Turkey, German proved to be very useful. We found people in Serbia who still remembered the Austrian Empire who were able to speak German. Then in Istanbul, we had all of the Gastarbeiter who had returned to Istanbul.

Zierler:

Yeah.

Lubensky:

So German was a better language than English at that time in Turkey.

Zierler:

Right, right.

Lubensky:

So yes, but German in science lost out. Later on French became important for me.

Zierler:

So how old were you when you left Germany?

Lubensky:

So I was… Let’s see. This would have been 1952, so I guess… Let’s see now. 1952. Yeah, so I was eight or nine. But now where did I go? In all their wisdom, the State Department decided to send us to the Philippines from the other side of the world, which was a new experience. So I was in third grade when we left Germany, so eight or nine, yeah, and when we arrived in the Philippines. At that time the federal government did not pay for the education of children of diplomats. So that meant we had to find a place that my parents could afford, and believe me, they were not well off. So we went to a Filipino school, which taught in English, called the De La Salle College, which is in the same group, you know, as the La Salle University here in the States that the Christian brothers run. So all of the instructions were in English. In fact, all the Filipinos I knew spoke very good English, including my best friend there whose name was Peque Gallaga, who spoke some Spanish at home still, which was a little unusual.

So we were there for two years, ’52 to ’54, and then we decamped to Spain under Franco when we were there, ’54 to ’56. I learned Spanish a little bit there—not as much as I should have because the American Air Force had just established an airbase in Madrid. So there were a fair number of Air Force people and there was an American school that I attended. Well, I started off in a British school, and then when the Air Force came, then I went to an American school. But in the Philippines, when we arrived, there were no desks left in the fourth-grade classroom where I should have gone, so they put me in fifth grade. So it put me ahead a little bit and probably had some impact on my upbringing.

Zierler:

Did you pick up Tagalog at all?

Lubensky:

No, no Tagalog. I can't… You know, that really wasn’t that useful. We had two servants who were from Cebu and Leyte, I think, which was farther south, and they didn't speak Tagalog. So the language was English, and we spoke English to them. So I didn't even… Even the kids at school did not speak Tagalog in front of me. They were all English-speaking, and the teachers… It’s really remarkable how quickly America transformed the language of the country. They had been 330 years under the Spaniards speaking Spanish, and Tagalog, of course, has a lot of Spanish in it at this stage. In a less than 50-year period, Americans changed everything. They set up an educational system in English, which eventually replaced Spanish as the principal language.

Zierler:

So how old were you when you left the Philippines?

Lubensky:

So I was 11, I think. Yeah, 11.

Zierler:

Where next? Where next?

Lubensky:

We went to Spain for two years, and I learned a fair amount of Spanish there. Then my father was sent back to the States to be in the Latin American Desk at the State Department. So I was able to finish high school in an American school in Wheaton, Maryland, ninth through twelfth grade, or half the ninth grade. I missed half of ninth grade when we were going to… Yeah, so that takes me through to college. My father, you know, he participated in writing the Antarctica treaties, worked on the Law of the Sea, things like that, and then he became a Latin American specialist, with assignments to Ecuador, Colombia, and El Salvador.

Zierler:

So at what school and at what time did you distinguish yourself in math and science to gain acceptance to Caltech?

Lubensky:

Yeah, that’s an interesting story. Really, my… Well, the education I got in the Philippines was pretty rigorous. They were old-school and they insisted upon doing things right. I did all right in math. I found it interesting when I was at that age, but in the Philippines—I mean in Spain, even, we just started off on elementary algebra in ninth grade and we left, and that was really kind of not very good. Then I went to Wheaton High School and I was several months behind. They were actually talking about putting me back in the eighth grade, but I was pretty gutsy at the time. I said, “I know I can do the ninth grade.” So I spent a lot of time really doing all the algebra problems and so forth. So I emerged at the end of the ninth grade, I think, at the top of the class. But there were no precursors that said I would do well. Back then people didn't worry about that that much, you know? Kids who were in grade school, well, you got grades, but mostly people were not uptight about how well you were doing in school and so forth. If you could read and do arithmetic, then you were okay. So I didn't feel any competition or any sense that I was somehow better able to do science than the other kids in the class.

Zierler:

Now was Caltech your dream or did you apply to a lot of top schools?

Lubensky:

So that’s the next part of the story. I had a good friend in Spain whose father was a brigadier general, and the father had a master’s degree in engineering at Caltech. My friend said to me one day, “Oh, Caltech is the best engineering school in the world. Let’s go there!” [Laughs] I mean it’s really odd how things happen because I decided that probably I did want to go to Caltech. But when I went…

Zierler:

But what did you know of Caltech versus Stanford, Berkeley, MIT? I mean you're on the other side of the world.

Lubensky:

Nothing. Nothing.

Zierler:

Right.

Lubensky:

Nothing. Nothing. But then the story continues that we arrived back in the States in ’56, and ’57 was Sputnik and everybody was talking about catching up with the Russians. So I really got very interested in astronomy. It started off with these books on the possibilities of space travel—actually, I managed to have one of them here—by Willy Ley I remember them. I don't know. This actually is not the original…

Zierler:

Oh, cool! Cool!

Lubensky:

…but this was the guy who wrote books about space stations, rotating things to give you gravity, and all of that. So when I was in ninth grade I read a lot of those. Then a little bit later on, just by accident, my father bought a book—it was on the shelf at a drugstore, I think—by Fred Hoyle called Frontiers of Astronomy. I don't know if you’ve heard of it, but it was really… You know, it was the story of the universe, so to speak. It turned out some of his views were wrong, but he got stellar physics and that kind of stuff right. I read that book cover to cover twice and decided that astronomy was what I wanted to do. So I took the $40 I earned as a bugler in a Boy Scout camp and bought a telescope I would train on the skies. So by that time then I knew that Caltech had Palomar and Wilson, and I thought, “Well, that’s where I want to go.”

Zierler:

Right.

Lubensky:

But you know, unlike today… Well, I applied to Columbia and got in there because there was a scholarship for children of diplomats. Harvard, of course, rightly turned me down, and then I had University of Maryland as a backup. But I did not live in a culture where people talked about that at all. I knew that I was going to go to college, but… My father even investigated whether I should go to Missouri Valley. I found that out later. That would have been a total disaster.

So I think that what happened… I think I graduated second in my high-school class because my gym grades were not as good as the girl’s gym grades. I did not go out for a team, and you couldn’t get an A in gym if you didn't go out for a team. [Chuckles] So I applied. I think the reason I got in was Caltech was trying to expand its horizons and they were interested in people from the East Coast. The interviewer who interviewed me was not a scientist. He was, I think, chairman of the English department at Caltech, and we talked about a possible diplomatic career for me and things like that as opposed to science. I think probably he put in a good word for me. The teachers probably wrote pretty good letters about me.

Zierler:

So you got to Caltech when? 1960?

Lubensky:

1960.

Zierler:

The original plan was to do engineering or physics or astronomy?

Lubensky:

No, I was going to do astronomy.

Zierler:

Okay.

Lubensky:

I arrived actually just the year before Feynman started teaching his course, so I didn't get that. Well, I’m not sure whether I would have survived that or not. I really did not know very much when I arrived there.

Zierler:

Had you taken physics in high school?

Lubensky:

Oh yeah, but we learned what a poundal was, you know? [Laughter] It wasn’t… It was sort of a joke. Chemistry was pretty rigorous. I learned a lot of chemistry there, and math--

Zierler:

So generally, compared to other students who had a more traditional high school background, how well prepared were you when you got to Caltech?

Lubensky:

I was not so well prepared, really. Freshman year was quite a challenge for me. I remember in chemistry we were learning mass-action laws. I couldn't figure those out, and I went to see the professor. This shows the difference between now and then. I said, “Look, you know. I don't understand this and I’m going to flunk unless you help me out,” and he said, “No, you're going to get it. Get out of here.” [Laughs] So I managed to figure it out, and at some level that’s the best thing to do to give me the self-confidence that I could make it. It’s not what we would do today. Today we would bring in all kinds of counseling and extra help and so forth.

Zierler:

Right, right. Now in those days, astronomy and physics was one department, two departments?

Lubensky:

No, it was a separate department, but at that time all freshmen -- physicists, chemists, mathematicians -- took essentially the same course.

Zierler:

Whether you were in physics or astronomy.

Lubensky:

Yeah. We had three hours of chemistry and six hours of chemistry lab a week, three hours of physics and three hours of physics lab, four hours of math, three hours of English, three hours of history, and three hours of mechanical drawing that everybody took freshman year, even the biologists. At that time, I guess biology was not so forceful. Now they don't make the biologists take the same courses that physicists take. So yeah, I came out of that all right in the end, and by the time I was a senior, I was in control of things.

Zierler:

Now when did you make the switch over to physics?

Lubensky:

Oh, okay. [Laughs] Of course, we didn't have to specify a major until the sophomore year. Well, so I liked astronomy, but I looked at what the astronomy people were doing, and the first course in astronomy involved doing things like calculating the corrections to the orbit of Mercury because Jupiter is there. They would run around with these cylindrical slide rules which gave them four-place accuracy. I just couldn't see myself doing that, so I stayed in physics. Caltech was funny in physics. It did not really recognize the field I eventually went into, namely condensed matter physics. That was not real physics, you know. You had to do particle physics and so forth.

Zierler:

Right. Now what professors in the physics department did you become close with?

Lubensky:

None. That was not… No. You see all of the kids today doing projects in high school and so forth. The Caltech undergraduate education was rigorous, and we clearly covered a lot more than most people did, than most other schools did, but this one-on-one thing… I did work with Prof. Eugene Cowan. One summer I worked in his Cosmic Ray Lab and it was just awful. I mean, he had a bank of scintillation counters and cloud chambers. He wanted dials to show how much charge was deposited by a cosmic ray shower… He would take a picture whenever there was an event and he would read the counters and show the cloud-cambers. You know, he’d have a picture of all the dials and that would be correlated with voltages, etc. that he had measured. I had to make the dials, but it was just me alone. You know, today, if you go out and work in a lab, you have a whole crew of people and it becomes a social experiment as well.

Zierler:

Right. So was your sense that the professors were really just not generous with their time with undergraduates, or just culturally it was not done to have that kind of interaction?

Lubensky:

I think the culture was that… No. Mostly, for the most part they didn't deal with undergraduates. At least that was my experience. I think it’s different now.

Zierler:

Yeah. Now did you develop an interest in the condensed matter experimental side of things as an undergraduate?

Lubensky:

No, no. I just followed what was in the text. I really liked the textbook by Leighton on atomic physics and so forth. That was the capping course of… So then I did well enough that I got accepted at Harvard, but not Berkeley…[laughs]…which everybody from Caltech wanted to go to. Stanford at the time was still considered a little bit of a joke, you know, a party school from where we sat.

Zierler:

Really! [Laughs] That’s interesting. Now I’m curious. It doesn't sound like you had so much direct contact with Feynman, but I want to know from your perspective to what extent his sort of larger-than-life personality set the tone for physics in general at Caltech.

Lubensky:

Oh, it was there pretty high. Yeah, I attended a couple of his freshman lectures. I attended what we called the alimony lectures at Hughes Aircraft when I worked there in the summers after I’d graduated. It gave rise to-- I don't know whether you know his work, but there’s this statistical mechanics book that arose from lectures he gave at the Hughes Research Center in Malibu… Well, it came from notes that students had taken. They call it his alimony lectures because, apparently, he was being paid enough to pay off his alimony to his second wife, I think it was, I believe. You know, the stories that we told about him were more about the playmates that he picked up in bars and things like that. [Laughs] You know, later on I got to know Mike Cohen, who was one of his students, and he would tell about their going to bars together and things like that. But he did develop that course, he and Leighton mostly, and I think there was another person involved. That, of course, changed the whole climate to the class after me. But in the end, even Caltech could not stay with it. They don't use that anymore, and they have not for years—decades, decades.

Zierler:

Yeah. So by the time you started thinking about applying to graduate schools, you really hadn't developed an identity as a physicist yet.

Lubensky:

Well, yeah. It’s so funny. At some time in our senior year, we had a meeting and a professor would say, “Well, here are some schools you might want to apply to,” but I knew nothing about them other than I’d heard of Harvard. But it didn't have the aura that it does now. I knew it was a prestigious place, but I would have preferred Berkeley at that time. So yeah, I didn't develop a… Well, I did work at Hughes Aircraft after my senior year. I worked in the laser development lab.

Zierler:

Had you considered entering industry and not pursuing a graduate degree ever?

Lubensky:

Yeah, I did consider it. I mean… You know, many, many of the people who go into physics are academic offspring, and they understand what the sequence is, understood what the sequence is. I had nothing. I understood, well, you go to graduate school. That sounded like the thing to do. They would have hired me at Hughes had I decided to do that. You know, that was… The ruby laser was invented at Hughes Aircraft and I was in that group for a while and the boss there liked me.

Funny experiences we had. One time there were two itinerant inventors from Texas who came and had this idea for… You have a ruby crystal with mirrors on the end, subject the crystal to a bright flash of light to produce a population inversion of states, which then emit light of a given frequency that bounces back and forth to produce a coherent mode that burns a hole in the front mirror to produce a pulse of laser light. These inventors thought that they could lase across large distances, so they put a big mirror on a barn door 100 yards away and turned on a laser with only a back mirror and got it to lase off the mirror on the barn. So their idea was this would be a good weapon for Vietnam. You point it at the jungle and you blind the enemy. [Laughs] I had to write the white paper on that and fix it up. The Hughes management were so excited that they sent it off and classified it as secret. I was only cleared for classified, so I couldn't proofread my own work. Then it came back from the Air Force as top secret, and of course I couldn't touch it. I have not heard of it since, so I imagine if fizzled.

Zierler:

Of course, of course. Any idea if McNamara ever laid his eyes on it?

Lubensky:

I have no idea, no. That was above my pay grade at the time, yeah.

Zierler:

So you get to Harvard the fall of ’64.

Lubensky:

Fall of ’64, right.

Zierler:

Okay, and what’s the scene there? How do you start to develop your identity as a physicist in terms of the courses--

Lubensky:

Well, everybody takes the first-year courses… You know, unlike now, there was a well-described two-year program, and for the most part you didn't start research until after you finished that. Then there was a qualifier and that kind of thing. I had said that I was going to do high energy experiments, but after spending the summer at Hughes Aircraft - Part of what I did at Hughes Aircraft was to try to make collimators and things like that in the machine shop, [Laughs] I decided no, that I didn't like experiment, so I eventually went into the theory. But I worked with Paul Martin there. At the time, his reputation was one of being really a tough guy when people he had…you know, really given a lot of people in their oral exams a lot of trouble, and he was not the most articulate of lecturers. But he wrote copious notes which I still use. So I approached him to work and he agreed to take me on. That was in the end a great move for me. … I learned later that my homework was better than most people’s, so at least there were TA’s who were giving advice Paul at that point.

Zierler:

What was Paul working on in those days?

Lubensky:

So he was still exploring problems using the formalism he had developed with Julian Schwinger (Nobel Prize with Feynman and Tomonaga in 1965), which was to develop a language that was inspired by field theory for many-body systems. He had had a series of students who were doing various versions of that—you know, itinerant ferromagnetism, response functions in magnetic systems, superfluids, phonons. Basically, he went down the list on all the things that you might have done. So the four, five, six graduate students who preceded me worked on that, and he was still thinking along those lines. But I have to say that he was in a kind of slump at the time. My thesis is probably the most embarrassing thing I’ve written, but it did… It was on hydrodynamics in magnetic systems, and unbeknownst to me—I think probably Paul knew about it—Bert Halperin and Pierre Hohenberg were working on similar things in a much more sophisticated way than I was at Bell Labs. And Paul did some work already on classical fluids. A contemporary of mine and Martin student, Dieter Forster, did some work on that with him.

Zierler:

So Paul essentially handed you your dissertation topic, or how much were you involved in developing the topic?

Lubensky:

Yeah, he handed it to me. Right. Well, yeah. We did a couple things that didn't go anywhere, and then he just decided I should take off. He was away in Paris for part of the time I was supposed to be working with him, so I didn't have too much contact until he got back. But there was plenty to learn, so it’s not as if I was being mistreated or anything like that.

Zierler:

Now in the late 1960s, obviously there was a lot going on campus at Harvard. Where were you in that? Were you aloof from that? Were you in the middle of it?

Lubensky:

I was mostly aloof. I had friends, of course, who were among those who occupied a college hall and all that. It had remarkably little effect on what I did, and most of my colleagues. We, of course, supported the more leftist side of things, but I was not a demonstrator, nor were most of the people in the physics department.

Zierler:

So when you defended, what were your options? What were you thinking was the next step at that point?

Lubensky:

Well, okay. So I was impressed that Paul had gone off to work at Orsay outside Paris on sabbaticals… I should say in 1967, I went to the Les Houches summer school near Chomonix and in the shadow of Monte Blanc, and I really liked that. Oddly enough, Harvard at the time had two language requirements, so I could have passed a test in Spanish in addition to German that I passed, but Spanish was not an acceptable scientific language. So I started taking French. I took two years of French at Harvard with the earphones and everything and came out speaking passably well. So if you learn German and Spanish when you're young, you have most of the pronunciations of European languages (other than those of the horrible Danish). So I could pronounce the French “u’, for example, which is the same as the German ü.

So I learned French fairly well, and then when I went to Les Houches, I was tossed in a cabin with a bunch of people, including Francis Meunier, who was French and had a car (a Trois Chevaux) which allowed us to drive around. So I spoke a lot of French with him, and I decided I wanted to do a post-doc there because, actually, a lot of Paul’s former students also had gone to Saclay or Orsay because Paul knew a number of the French people. So I decided that I wanted to do that and I applied for an NSF fellowship and got a fellowship for one year.

Zierler:

Now was the NSF fellowship the only way that you could have put that opportunity together, or were there other possible sources?

Lubensky:

I think it would have been difficult. It would have been easier later on when the French started opening up, you know, paying for it or something, but I couldn't have done it without the Fellowship… And it was only one year. You know, today they’ll usually give you two years in an NSF grant.

Zierler:

Right, right. Was the game plan to continue refining your dissertation or were you looking to go onto other projects?

Lubensky:

Well, I was supposed to work with a guy named André Blandin, who was a magnetism person. So since I’d done a thesis on hydrodynamics in magnetic systems, it sort of was a natural thing to do. I knew a fair amount about that, but the winds of history do funny things to you. I arrived at Paris, at Orsay in, I think it was June of 1969.

Zierler:

Yeah, ’69.

Lubensky:

’69, yeah, and France was still feeling the effects of the ’68 revolution.

Zierler:

Right.

Lubensky:

So the group I was supposed to work with was just dead. Blandin, who had been one of these guys who rose very rapidly in the ranks, found himself on the wrong side of the barricades, if you wish.

Zierler:

Yeah.

Lubensky:

He was upset because he was in the establishment. He had identified himself as a gauchiste and it really got to him. Eventually he committed suicide. So again, luck of the draw, when I was at Les Houches, de Gennes (future Nobelist) was lecturing in French because he was protesting against the American things in Vietnam. It turned out he had a classical guitar, and so I went and I got to play his guitar a little bit. So he knew who I was and I knew who he was.

So when I was in my office at Orsay in the very beginning, he came and said, “I know you! Come to dinner!” He had this house at the bottom of the hill. I don't know if you’ve been to Orsay, but it’s on the Ligne de Sceaux. The condensed-matter building (Bâtiment 510) was up on a hill. Down at the bottom of it, very near the Le Guichet station, was the de Gennes residence. So I went to dinner at his house, and he was just setting up the liquid crystal thing, and that was really an opportunity that was just a gift from heaven, so to speak.

Zierler:

This is your first interaction with liquid crystal?

Lubensky:

Absolutely. I mean, liquid crystals were nonexistent in the physics world until de Gennes came along.

Zierler:

Right.

Lubensky:

There were chemists who fiddled around with it a little bit. There were a few mathematician types, applied mathematicians who--

Zierler:

So what was his access point to liquid crystals? Was he coming from an experimental side or from a theoretical side?

Lubensky:

Well, he was theoretical. So early on he worked on magnetism and superconductivity. He was a post-doc at Berkeley where he got into that, but also earlier on in the late ’50s he did some work on polymers, so he was aware of “the soft side of things.” In the ’67… Let’s see. In ’67 at Les Houches, he lectured on superfluids and superconductivity, and I was not aware of any liquid crystal work he was doing then. But by ’68 he had created the liquid crystal group at Orsay, that actually published papers with sole author “Groupe d'Etude des Cristaux Liquides (Orsay).” No names of people, just the group.

Zierler:

Yeah. In those early days, what was so exciting about liquid crystals? What would liquid crystals allow people to do?

Lubensky:

So the thing that was really intriguing about liquid crystals is it provided a whole host of new systems which had different symmetries. Until liquid crystals became known in the physics community, you had fluids, gases, crystalline solids, and amorphous solids, right?

Zierler:

Mm-hmm [yes].

Lubensky:

And the range of interesting symmetries available there, even though there are 230 space groups of crystals (Figure 1), they all have to do with arrangement of atoms in space. So along comes liquid crystals and you get this thing that breaks rotational symmetry and nothing else. It’s a liquid, but it has properties that are something like a magnet. Then you can have smectics. You get these layered structures. You have smectics in which the molecules tilt this way (away from the layer normal). Each one has a different symmetry and a different set of what you could call Goldstone modes that arise from the broken continuous symmetry. So this was a playground for a theorist. Fortunately, after I was in Orsay, new experimental tools, particularly new x-ray scattering facilities, which were ideal for probing liquid crystal structure and fluctuations, came on board. Those and light scattering were together able to test and verify new theories, and chemists kept finding new materials with new and unexpected symmetries. This created a wonderful interdisciplinary environment to do science.

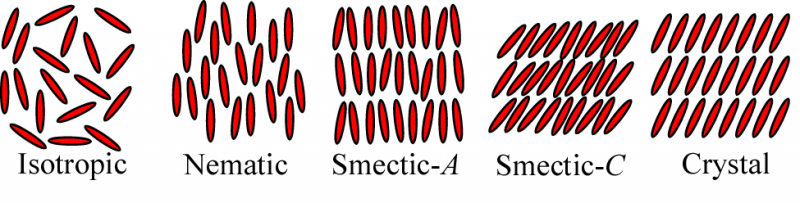
Figure 1: Phases of liquid crystals formed from bar-like molecules.  The isotropic phase with molecules at dynamically random positions such that the system looks the same under arbitrary translations and rotations.  The molecules in the nematic phase are still at dynamically random positions, but they are aligned on average along a single axis, thereby breaking the rotational invariance of the isotropic phase.  In the smectic A phase, molecules are arranged on average in layers, thereby breaking translational symmetry.  In the smectic-C phase, the molecules tilt away from the layer normal, and, finally, in a crystal, molecules sit on average on a crystal lattice.

 

Zierler:

Were there any immediate theoretical implications based on what liquid crystals were able to do?

Lubensky:

Oh, yeah. Well, it was more really fundamental understanding that went on. So when I was at Orsay, I had some experience doing hydrodynamics, and there was this theory of the dynamics of the nematic phase developed by the continuum mathematicians Leslie and Ericksen where they posited that you had a system that had pointless arrows that had aligned. So they said, “Well, let me imagine I have a unit vector, [

] , called the director in liquid crystals, that can vary in time and space. I’ll say, ‘Oh, it has a kinetic energy which is [ ]and then you have some kind of elastic energy that tells you about how much energy it takes to bend the director or twist it, etc. So it had the smell of things that you see in crystals, but the important thing is that in the nematic you’ve broken a continuous rotational symmetry, and that immediately implies that you have low-frequency modes. The high-energy people call them Goldstone modes, which are massless particles that are a consequence of a broken continuous symmetry, and so you could actually put things in field-theoretic language and show that you had to have a mode that had zero energy.

So then the question was, “Well, once you’ve got that information, how do you develop the dynamics that tell you what goes on away from the zero frequency?” The argument goes like this: It takes no energy to rigidly rotate the sample, but it does const energy to say perturb the system with a long wavelength modulation of the direction of order. Infinite wavelength is equivalent to a rigid rotation. Continuity then implies that the distortion energy should vanish as 1/(wavelength)^2, So as wavelengths get longer and longer, both energies and characteristic frequencies become smaller and smaller.

So I got in… Well, I should say that at the time, Bert Halperin and Pierre Hohenberg at Bell Labs were developing sort of a consistent theory which they applied to magnets and to superfluids. I found out that they were doing that work in France, but there was no way I could get their preprints. I developed my own theory which relied (a little more heavily than I would have liked) on the Leslie-Ericksen theory that I pointed out had inconsistencies, which to this day is not admitted by that community.

As luck would have it, at the same time Paul Martin comes back into the game with Peter Pershan (of Harvard), who did experiments, and then there was David Litster at MIT. So Paul developed a hydrodynamic theory of liquid crystals which was not the same one as the Leslie-Ericksen. So when I returned to the States since I had a post-doc at Brown, we were working on the same thing. His first theory was wrong, it turned out. He missed an important fact, and once I got a hold of the Hohenberg-Halperin approach, I realized what it was.

Actually, Dieter Forster, who was another student of Paul’s, was at Chicago when I went to give a talk there. I told him all my thoughts on it and he said, “No, no. It’s not going to work.” Eventually he came around and we were preparing a paper on the hydrodynamics of nematic liquid crystals. It turns out that Paul and Peter and Jack Swift had done the same thing, basically, so there was a paper written with all five of us with… You know, you could imagine the Harvard people apparently taking more credit—not on purpose, but…

Zierler:

So Tom, if we could zoom out for a second, it sounds like the ten years essentially that you spent at Caltech and Harvard were not nearly as formative as the one year you spent in Paris.

Lubensky:

Absolutely, yeah, in terms of directing at something that was-- I mean that was really exciting times because you had all of these things, and then of course Paul then goes off to Saclay again and he writes the definitive paper on broken symmetry hydrodynamics of all systems, smectics, etc., etc. I had done the hydrodynamics of the cholesteric phase, which is a phase consisting of chiral molecules whose director rotates in a helical pattern as shown in Figs. 2 and 3. So you have a helix and it’s sort of a layered structure. It turned out those dynamics were very similar to what you get in a smectic layered structure.

Then along comes two other things. First of all, I spent a year at Brown. This was just at the beginning of the renormalization group, and I was still working alone to get my cholesteric paper done. Leo Kadanoff, who had just moved to Brown from Illinois, was doing city planning. You know, he was going to use all of his mathematical prowess to solve the problems of the city. Basically, though, I was supposed to be his post-doc. We did not interact on physics very much, and I was even unaware that he and Franz Wegner, then also a postdoc with him, were working on what turned out to be a very important paper on the foundations of the renormalization group.

Figure 2:  left: a chiral molecule.  It cannot be made to coincide with its mirror image. Right: two chiral molecules want to rotate relative to each other.

 

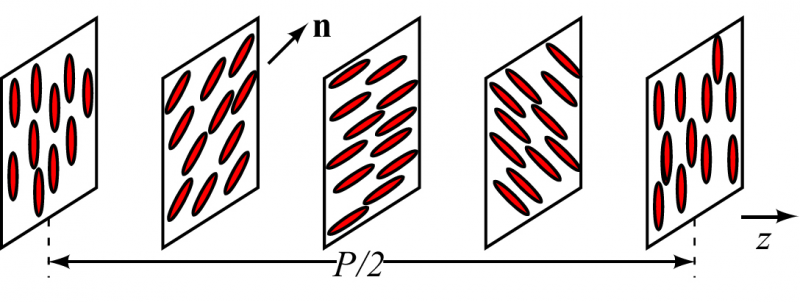
Figure 3: Schematic of the cholesteric phase in which molecules rotate to form a twisted pattern.  Repeated planes of molecules with the same orientation can be viewed as layers similar to those of the smectic phase.

They had gotten the notes by Wilson, and they were working on making it a little more formal, etc. I did not know that they were doing that. I got a position at Penn, and I knew that all the people I respected were jumping into the renormalization game—you know, Hohenberg and Michael Fisher and Martin and all those.

Zierler:

Right. Now you came to Penn as an assistant, tenure line, right?

Lubensky:

Assistant professor, right. 1971 I guess I arrived, yeah. So it was clear to me that I should get into the renormalization group game. So that’s one thing. The other thing that happened was that you could carry out these precise measurements on liquid crystals, so there were critical phenomena associated with liquid crystals.

Zierler:

So Tom, I want to ask you, before we get to the specifics of the research, your impressions of Penn in those early days. Was this a department that was up and coming and was looking to establish itself among the bigger players? What was your sense of what was going on in those days?

Lubensky:

Okay. First impressions of Philadelphia. [Laughs]

Zierler:

Right. [Chuckles]

Lubensky:

I arrived at the airport--

Zierler:

Not just Philadelphia, west Philadelphia.

Lubensky:

Right. Yeah. You know, the road from the airport into town passed a metal junk place. Oh my god. When I went to Brown, I was sort of guaranteed a position as an assistant professor after the post-doc tenure, but they were unwilling to give it to me after a year. In the end Penn was an excellent match for me. So yeah, Penn was a funny place at the time. It certainly was not amongst the best known places, but remember Bob Schrieffer was there, a Nobel laureate (along with Bardeen and Cooper) for their theory of superconductivity, and a few younger people like Alan Heeger, who eventually got the Nobel Prize. It still had a nuclear program, which was considered one of the better ones, but people had begun to stop paying much attention to nuclear physics. It had a… You know, they were still running the Princeton accelerator in high energy physics and Penn has a substantial presence there, but it was not considered amongst the very elite. Younger hires in particle experiment eventually undertook leading roles in the LHC and other accelerators. In the end, that was good for me. Had I stayed at Brown under the shadow of Kadanoff, I doubt I would have emerged from my cocoon, so to speak. So it was really a great place for me.

Penn had and still has something called the Laboratory for Research on the Structure of Matter (LRSM), which is still running, continuously funded since 1960, when it was funded first by the Navy. Eli Burstein was the one who set that up, and he had the vision that there’s something called materials science and engineering which brings together the solid state physics that physicists looked at, but you also had lots of engineers in materials and people who began to call themselves material scientists instead of metallurgists. So there’s a metallurgy department that became eventually the material science department. The LRSM encouraged a certain amount of interdisciplinarity which grew with time. That was a plus, but I did not appreciate at the time how much of a plus it was. It did eventually provide some support for me, though… Oh, and then Herb Callen was there, who had a big name in magnetism. And there was Henry Primakoff, whom you may have heard of.

Zierler:

Sure!

Lubensky:

He was sort of the grand old man of the place who could do everything. There was Mike Cohen, who was probably the smartest guy that I’ve known. He was one of these guys who could solve all of the electromagnetism problems and quantum mechanics problems and stat mech problems, and he would delight in coming into your office and posing a problem and then leaving. You think, “If I don't solve this, I will be labeled an idiot by Mike Cohen.” Yeah.

So it was a good place for me. You know, the people were very supportive. Bob Schrieffer was. I watched them develop (he and Alan Heeger and W.P. Su, who was a postdoc if memory serves me correctly) the theory of the one-dimensional conductors, you know, TTF-TCNQ , polyacetylene and all of that, which eventually contributed to Alan’s receiving a Nobel Prize in Chemistry along with the chemistry collaborators Alan MacDiarmid and Hideki Shirakawa. They were one of the first to confront the issue of what is now called topological band theory. The model that they invented—it’s called the Su-Schrieffer-Heeger model—is a real workhorse. It’s used now for the topological insulator language to start off and explain how topological properties can control physical response and so forth.

Zierler:

Now are you mostly focusing on a single line of research or are you involved in multiple projects and research endeavors at this point?

Lubensky:

Well, over my life, many different ones.

Zierler:

Yeah.

Lubensky:

For the last several years, I’ve been working on topological mechanics, but I’ve now switched to doing what’s called odd viscosity systems. So I don't know how much you want me to go down the history of what I’ve done, but I’ve been at it for 50 years, so it’s… [Laughs]

Zierler:

No, no. Very much. I mean, roughly right now. Let’s go from… So for example, you were tenured in 1975; you were named associate professor in 1975.

Lubensky:

Yeah.

Zierler:

So was your sense… I mean it’s always a good way to think about these things. Was your tenure in recognition for a specific research endeavor, or was it sort of the sum total of what you had accomplished, in recognition, up to that point?

Lubensky:

Well, I think it was more four things collectively that I had done: hydrodynamics of liquid crystals and renormalization studies of critical phenomena in semi-infinite systems, of superconductors and smectics, and of random systems. So I did manage to read through Wilson’s notes, and I had a really great Penn colleague, Mort Rubin, who was a particle theorist who wanted to get into the renormalization-group game as well. At the time, Schrieffer and a number of other people at Penn were doing surface science, which was then a fairly new field (to physicists at least). Phil Anderson had pushed it and Schrieffer did, so I attended some of their lectures. It occurred to me that it might be possible to apply renormalization-group ideas to surface phase transitions. And then I’d seen a paper by Hohenberg on critical phenomena on surfaces terminating a bulk sample. So I was able to do the Wilson calculation on surfaces. Mort and I did the first renormalization group calculation of a semi-infinite system. Then we wrote a very extensive review-article type paper on the mean-field theory of surface phase transitions, which was actually reasonably complicated.

I had the good fortune to go to Aspen in the summer of ‘73 I think it was. Let’s see. Yeah, ’73. Because of my interest in the renormalization group and my knowledge of liquid crystals, I had done some renormalization group-like calculations for liquid crystal models, and in particular the smectic phase. There was this famous analogy that de Gennes introduced that showed that the established a mathematical connection between smectic liquid crystals and superconductors. I worked out the renormalization group for the superconductor, and then I tried to do it on the liquid crystal, and it didn't work for either. But I was still just playing around. What I found was there was no stable fixed point for the superconductor.

When I went to Aspen, Bert was there, and he suggested we work on applying the renormalization group to the superconducting transition. So I sort of sheepishly said, “Well, I’ve sort of done that. I didn't get a second-order transition.” But I went back to my office and very carefully went over my calculations again, and I told Bert about them. That was quite an experience for me. We were sitting in his office at Aspen, and Bert finally heard what we said, and he sat there stroking his beard. It must have been ten minutes. Then he coughed off the reason we were getting no fixed point and the whole theory and everything. In sort of a complete, straight argument from beginning to end, he explained that there was a first-order discontinuous transition rather than a second-order continuous one. We found that if you generalize the theory to one with n complex components rather than a single-component complex field, we could get a second-order transition. Shang-Keng Ma was there at the time also, and he joined our collaboration. He is known for his stat mech book. He unfortunately died about ten years thereafter.

Then Bert and I did the liquid crystal. Again, Bert’s insight was really something. It turns out that in superconductors only gauge-invariant quantities can be measured. But in liquid crystals, you can only do measurements in one gauge, and that gauge turned out to be a very singular one that gives rise to all kinds of peculiar properties that are clean in the theory, but still have not been completely verified experimentally. A lot of people have spent a lot of time on this problem without success. So there’s a system that has some of the most beautiful theory that you can imagine that still does not match experiment.

Zierler:

Now this very dramatic scene of silence and beard stroking and then stream of consciousness—were you… I interviewed Bert, so it’s very--

Lubensky:

Mm-hmm [yes]. The same thing here.

Zierler:

Well, I mean it’s very interesting to hear your perspective on this. But did you feel like you were witnessing like a eureka moment in real time right there?

Lubensky:

Yeah, yeah. I mean… I already knew… First of all, Pierre Hohenberg and I had talked to a couple of times and he said, “Well, you know, when I was at Bell Labs I had this secret weapon”—namely, Bert—and Pierre would get invited to give talks. He would say, “I don't know. You should have Bert give it.” “No, no. We want the lead guy,” but really it was Bert. And you could tell. The papers that Bert wrote were just crystal clear. There was no obfuscation, you know. He just came out and said it. So I already was in awe of him, so to speak, and I was pleased he approved of the talk I gave at Aspen on my work on semi-infinite systems.

And then when we worked on the liquid crystal thing, we still did not have it perfectly right. So when I went back to Penn and he was at Harvard, we used to have these long phone calls, and we’d get the same thing. At some point there was something unclear and there would be dead silence at the end of the phone. “Bert, are you there? Are you there?” [Laughs] But he got it right. So those were really new departures. I had done the hydrodynamics of the nematic phase, the first renormalization group on the semi-infinite systems, the phase transitions in the liquid crystals, and then doing the liquid crystal thing, I developed a model for a phase transition where your order parameter… I don't know how versant you are in all of this.

Zierler:

I’m a historian of physics. I’m not a specialist in any one area, but I eat this stuff up, so tell me, please.

Lubensky:

So there are lots of models that Wilson and others introduced.

Zierler:

Right.

Lubensky:

And the different models had different symmetry properties and so forth, and they fell into different, what they called universality classes of critical exponents.

Zierler:

What does that mean, universality classes?

Lubensky:

So that means these things have the same symmetry exhibit critical phenomena controlled by the same mathematical fixed point.

Zierler:

What’s the significance of that?

Lubensky:

Okay. So the thing that Wilson figured out is that near a critical point-- Actually, I should say that Leo Kadanoff, Michael Fisher, and others had really figured out the phenomenology of what goes on near a critical point prior to the Wilson theory, So you have this vast phase diagram, and the whole theoretical world at the time was focused on the one point (or line) where there was a phase transition. That’s because in the vicinity of that, you get something that’s scale invariant. So you start off with something that has a length scale, which is the inter-particle spacing or something like that, but as you get closer and closer to the critical point, that length scale becomes unimportant because it’s compared to a very long length scale, associated with developing order. The critical properties (critical exponents, etc.) are the same for all systems controlled by the same fixed point.

So Wilson, and others that followed, showed mathematically that you can have a whole series of models that have different symmetries. For example, you can have a vector that has two components, so that’s the universality class of the superfluid. Or you can have a vector that has three components. That’s a ferromagnet. Or you can add a term in the potential energy that introduces some sort of point group symmetry that’s different from continuous variation and so forth. So you have the Ising model where the a vector can only point up or down, or you can have an xy model where the vector can spin around on a circle, or you can have the O(n) model where this vector spins around an (n – 1) dimensional sphere. So the liquid crystal, the nematic has a property that it breaks rotational symmetry. Its director can point anywhere on a unit sphere, but opposite sites on the sphere are equivalent as shown in Fig. 4.

 

Figure 4: Schematic of the director field in a nematic.  It can point anywhere on a sphere (left) but opposite points are equivalent as indicated by the red dots in the right figure.  A path in real space maps the director to a path such as the closed loop in the figure.

 

Zierler:

Okay.

Lubensky:

So that’s not a vector. You need something else to describe it, and it turns out that a symmetric traceless tensor is what’s needed, so I don't know how much you follow the tensors. I developed a theory with a graduate student at Penn, Richard Priest, on what the critical phenomena, if any, symmetric traceless tensors exhibited. Oddly enough, we found that this system has under appropriate conditions a universality class that became non-trivial below six spatial dimensions. This observation, as we shall see, turned out to be important later.

At about this time, a Penn colleague, Brooks Harris, and I applied the renormalization group formalism to the problem of phase transitions in random systems - for example for an Ising or O(n) model in which the interaction energy between neighboring spins is a random variable. This effort was a result of Brooks’s interest in the problem and a very fruitful conversation we had with Ken Wilson, who suggested we should treat the variance of the random interaction energies the same way that we treated the non-random components of the theory. This work turned out to be quite influential: many theorists extended our work and there were experiments to verify and extend our conclusions.

By early 1975, I had developed a new hydrodynamic theory of nematic and cholesteric liquid crystals and applied the new Wilson renormalization theory to the superconducting and nematic-to-smectic transitions, to semi-infinite systems, and to random systems. I had done all of those things before I was promoted, so I think it was a fair promotion.

Zierler:

In what ways was the Potts model relevant to your work?

Lubensky:

Now to continue the story of the unexpected utility of the “toy-model” calculations Priest and I did: Shortly after my promotion to Associate Professor, we had a visitor, W.K Holcomb, who was interested in percolation, and there were a pair of mathematicians, P. W. Kasteleyn and C. M, Fortuin, in Holland who had shown that the s-state Potts model… So a Potts model is a one in which you have a vector that can point in s different directions. The simplest Potts model has three states: the vector can point to the vertices of a triangle. You can go up and do it in three dimensions and it points to the vertices of a tetrahedron, and you can generalize that to s dimensions. So it turned out--

Zierler:

And that’s how you get to six dimensions?

Lubensky:

Well, the six dimensions refer to six spatial dimensions… And s specifies the number of degrees of freedom of the order parameter, not the dimension of space (but eventually we get there).

Zierler:

Okay.

Lubensky:

Let’s see. Where’s my train of thought now? Yeah, so this Dutch pair had shown that if you take the limit that s goes to 1…where as indicated, s is the number of components, so if you have an Ising model in which a unit-length vector points either up or down… It has two states. The one-state Potts model is an analytic continuation of a series of physical models with components like a triangle or a tetrahedron that you can draw or build a model of-- But they took a limit in which you went to a value of the parameter for which you cannot really draw a picture of. It turns out that you can write down a field theory for an arbitrary s-state Potts model; and the s = 1 limit describes percolation which is process of creating a sample-spanning cluster of linked bonds as they are randomly added to a lattice grid. Alternatively, you come from the other end by removing bonds from a full lattice -- eventually at a critical probability you lose the sample-spanning cluster, leaving only isolated ones. As you decrease the number of bonds, you decrease the probability that you're in that cluster, so that probability plays the role of an order parameter.

It turns out that the liquid crystal models I had studied with Priest already contained the 1-state Potts model and, therefore, describe percolation, and from that work, we (my Penn colleague Brooks Harris and Holcomb) were able calculate the critical properties of percolation in a 6-[epsilon] expansion about six spatial dimensions. You know, that opened the door to a whole new class of problems.

Zierler:

How did you conceptualize your work as it related to sort of broader questions in physics? I mean is your… I mean, this is as much a question of the way you organize your thoughts as it is, you know, your identity as a physicist. Did you tend to think of what you were doing as an island in and of itself—that this is just your research area; these are the things that you were focusing on? Or did you try to think about ways that this might apply to larger, more foundational concepts in physics?

Lubensky:

Well, you know, I won't go so far as to say I gravitated towards SU(3) and nonlinear gauge theories and all of that stuff of high energy, which the high energy people and to some extent the quantum people—I do more soft physics—they look down upon people who actually had a system to look at as opposed to the abstract.

Zierler:

[Laughs] That’s a fair point.

Lubensky:

But I always had my eyes open for applying my knowledge to different things and to concepts that were more general than deeply specific, and often it’s in a way that’s surprising. Let me see. For example, later on when I interacted more with experimentalists, we actually were amongst the first to introduce liquid crystal colloids and emulsions. One of the things that’s exciting about the liquid crystals, as I said, is this topological business, so by that I mean you can have structures that form that are characterized by a topology and you can move things around geometrically, but you don't lose it. So for example, if you have a vortex in a superfluid where the fluid is flowing around a central core (like that – showing with hand motions), you can't get rid of that without somewhere destroying the order, and so that’s topologically protected, we say.

Zierler:

Yeah.

Lubensky:

And liquid crystals have symmetries that are more complicated. The one with the nematic, you have this axis that doesn't have an arrow – think of it as an arrowless vector. The axis can wrap around a sphere, but diagonally opposite points on the sphere are physically indistinguishable.

We studied defects in the director in mixtures of liquid crystal, water, and a surfactant [Poulin, Stark, Lubensky, Weitz, Science 275, 1770 (1997)]. They would form vesicles in water enclosing the nematic liquid crystal [Fig. 5] or inverse vesicles containing water in a nematic background [Fig. 6]. In the former case, the director points along radius vectors if there is a small water droplet at the center. If the latter case, the boundary conditions say that the axis must point perpendicular to the outer spherical surface. We trapped a defect where the configuration of the nematic look very much like that of the electric field around a point charge. So one of the things that happens, if you put a water droplet surrounded by a surfactant in a nematic where the vector is pointing away from the droplet surface, the droplet says, “I want all of my axes to point normal to the surface of the spherical water droplet. But the rule says, “When I’m far away, I don't have any defect,” so to meet the boundary conditions both at the droplet and at infinity, the system has to pull out another defect that compensates for the defect that comes from the boundary conditions at the droplet. So what you get is this sphere with the arrows coming out, and down a point defect that compensates for this so that at large distances, the directors are parallel as shown in Fig. 7.

Figure 5: A nematic droplet (mostly pink) in water (black) viewed through crossed polarizers. At the center is a small water droplet. The boundary conditions are that the director be perpendicular to both the inner and outer surfaces creating a configuration that the director always points in the radial direction.

Well, we wanted to understand how we could describe the energetics of that. So I remembered that the compensating defect looked just like the zero of an electric field when you place a spherical conductor in a uniform electric field. In fact, we were able to use that image taken from a junior course on electromagnetism to advance our understanding of liquid crystals. So that kind of thing goes on all the time.

 

Figure 6: The large black circles are spherical water droplets in a nematic. The small black dots between them are the point defect drawn from the nematic to keep the director parallel as shown in Figure 7. 

 

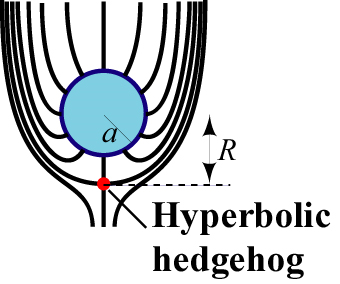
Figure 7: Schematic of the director profile around a water droplet in a nematic. Note the director emerges perpendicular to the droplet surface. Below the droplet is a point defect called a hyperbolic hedgehog. The director changes direction so that is aligned along the vertical axis far from the droplet. This configuration is essentially the same as that of the electric field when a conducting sphere is placed in a uniform electric field.

 

Zierler:

Tom, were you ever… How much, if at all, were you concerned or interested in the applications of your research beyond sort of the environment of the physics department or the lab? I mean were you thinking how this research might be adopted in industry or beyond your immediate world?

Lubensky:

Yeah. You know, one thinks about it. It’s certainly not my strong point. I have collaborated a fair amount with experimentalists, so one of the things that I’m known for now is the theory of what they call microrheology. So rheology is the study of the flow of fluids and the resistance to it and things like that. If you go to the microscopic scale and you want to know what happens at 1 to 10 or 20 ?, it’s hard to do a standard rheology experiment where you put things in a rotating cylinder and spin it.

Zierler:

Just because the scale is too small?

Lubensky:

Yeah, yeah. So Tom Mason and David Weitz, who were working at Exxon at the time, showed that the complex viscosity of complex fluids, like polymers or emulsions, could be determined by measuring the time-dependent fluctuations of a colloidal particle suspended in the fluid of interest. This technique allowed the measurement of rheological properties of small quantities of a fluid using light scattering (to measure particle fluctuations) rather than by traditional mechanical rheometers. John Crocker, who was a post-doc at Penn and eventually a faculty member at Penn, was interested in finding out what happens inside a living cell. Can you measure the rheological properties of a cell? It turned out that they were better off measuring …. Let me just see how I say this right. The correlated displacement of two particles instead of that of one particle provides a better measure of viscosity because the particles themselves perturb the medium around them, thereby modifying the local viscosity.

Well, it turns out that that problem is essentially the same thing as the difference between the mutual capacitance and the self-capacitance of two spheres. So if you have a sphere that’s put in a dielectric fluid and the metal sphere causes a sheath to form around it that’s different from the surrounding fluid, then your voltage to ground is surely different from what it would be if you had the unperturbed fluid all of the way to the sphere. On the other hand, if you measure the mutual capacitance, you see the fluid around it and you don't see the sheath.

So starting from there, we developed a theory for this microrheological process, and it’s used extensively to study rheological properties of complex fluids, etc. So I don't know if anybody’s made money on that, but certainly there are lots of experimentalists who use that technique.

Zierler:

I’m thinking specifically of your long-term partnership with Exxon in the early ’90s.

Lubensky:

Yeah. So that came because Sam Saffron, who had been on the Exxon staff for someone time, left to take a job at the Technion in Israel. Exxon decided it need to fill the vacant position, and I was offered a semester-long temporary appointment there, which I took. I later was a consultant for several years. There I worked with a postdoc, Fred McIntosh, on things that were related to the petroleum industry. In particular, what happens when you have an ordered surface? So suppose you have a vesicle consisting of a surfactant that forms a bilayer that covers a sphere, separating an aqueous interior from a aqueous exterior, and the molecules of the surfactant want to tilt relative to the normal to the sphere, i.e., to the radius vector as in the smectic-C of Figure 1. Then you’ve developed on the surface a broken symmetry of the xy type I just described with a vector field on the surface, and the “Hairy-ball” or Poincaré-Hopf theorem, which says that the field has to have sources or sinks, i.e., cowlicks or more mathematically topological vortex-like defects. If you have something that’s ordered on the surface, you have to have two poles. But then if you make it so it’s not just an xy model, but you make it a model where the order parameter is a two-dimensional vector-like object that is identical to itself after a rotation by 60 degrees rather than by 360 degrees as in a standard vector or by 180 degrees as in the nematic director, then you have hexagons that move around, and you will have not 2 defects, but 12. So we developed a theory of that, and we extended some work I’d done with Jacques Prost in Paris.

Zierler:

Now I see that there is a recurring theme. You keep going back to France.

Lubensky:

Ah yes, la France. It’s actually sort of sad. France was the center of the soft matter community throughout the ’70s and ’80s due largely to the influence of Pierre-Gilles de Gennes, but it is less so now.

Zierler:

Now were you unique among his… I mean, did he have other American—I don't know what the right word is—mentees, acolytes? I mean were you--

Lubensky:

You mean de Gennes?

Zierler:

Yeah. As an American, were you unique among that crowd?

Lubensky:

No. Let’s see. Phil Pincus, now at USCB certainly had a much closer relation with de Gennes than I did. Tom Witten of Chicago probably had a more intimate relation that I had because they actually collaborated and co-authored papers.. De Gennes did, however, mention me in his Nobel Prize speech, which was very uplifting.

Zierler:

Sure.

Lubensky:

I did something called the twist-grain-boundary phase.

Zierler:

Mm-hmm [yes], mm-hmm [yes].

Lubensky:

You know if you put a magnetic field on a superconductor, you get the Abrikosov lattice of superconducting vortices. So I remembered the de Gennes theory of the smectic said that the layered structure can be described by a mass-density wave characterized by a complex field, with an amplitude and a phase, that is the analog of the complex order parameter of the superconducting phase. In addition, the director n, specifying the direction of molecular order, is the analog of the vector potential of the superconductor. The question was what is the analog of the Abrikosov phase? My graduate student, Scott Renn and I (with some input from Jim Sethna of Cornell) managed to develop a theory of the analog of the Abrikosov phase in the liquid crystal. What happens is that the molecules in a smectic doped with or composed of chiral molecules (which cannot be superposed on their mirror images) wants to twist like those in the cholesteric phase. But the smectic has layers that do not want to twist. It’s like trying to twist the French pastry, mille- feuilles (a thousand leaves), you get a mess. You have to break the layers. So what happens is that you make grain boundaries, separating regions of layered order with differently oriented layer normals, and you have a series of grain boundaries that give you discrete jumps in orientation. As luck would have it, after we did that theory, almost simultaneously a group at Bell Labs saw it independently experimentally, so that was really quite exciting.

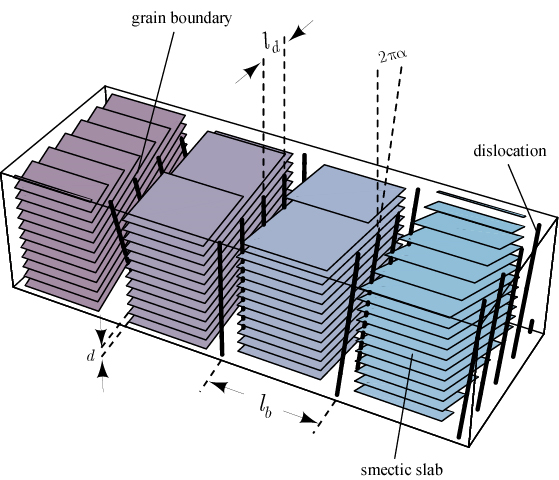
Figure 8: Schematic of the TGB (Twist-grain-boundary) phase.  The director is normal to the layers that come in blocks separated by grain boundaries that themselves consist of topological line defects called screw dislocations.  The director and thus layer normals undergo discontinuous rotations across the grain boundaries.

 

Zierler:

Now this is interesting. You keep coming back to what Bell Labs was doing and--

Lubensky:

Oh. Well, you know Bell Labs was perhaps the US’s leading center of condensed-matter science at that time.

Zierler:

Of course! No, so I mean my question there is it’s almost like... I mean, if you're competing with research that’s going on at Bell Labs, you almost have like one hand tied behind your back, right?

Lubensky:

Yeah. But it must be said that in this case, Bell Labs came to my aid. It did the experiment that proved my theory.

Zierler:

I mean, it’s an entirely different budgetary environment; the opportunities for collaboration there. I mean it’s a totally different way of doing research.

Lubensky:

Right, right. Yeah, and it was really good for the community, though. People who weren't at Bell Labs would often get angry with them for the power they had, you know. They had a Phys Rev Letters factory, basically.

Zierler:

Right. Did you ever consider jumping ship and joining Bell Labs, at least in the earlier years?

Lubensky:

Well, I was not made an offer at Bell, no. I would not have jumped ship. I played footsy with one or two other places, but in the end… You know, Exxon offered me a job sort of, but they were really not ready for it.

Zierler:

Yeah. So those are the pole factors, but I wonder on the other side how much you enjoyed—you know, beyond the pure, the basic research, how much you enjoyed teaching at Penn and being a mentor to graduate students.

Lubensky:

Yeah. I certainly enjoyed both. I enjoyed teaching graduate students what eventually became the book, Principles of Condensed Matter Physics, that Paul Chaikin and I wrote. I think, if you're honest, that my success with graduate students is not what many of my colleagues have. I haven't produced that many students who have really done outstanding work. I’ve done better with post-docs.

Zierler:

So who have been some of your most successful collaborations with post-docs?

Lubensky:

Let me see now. So I have a long-standing relation with Sriram Ramaswamy. He was a post-doc with me in the mid ’80s when we worked on quasicrystals together. Yeah, so that’s the longest-standing one that I’ve had relations with.

Zierler:

Where did he go after Penn?

Lubensky:

He went to the Indian Institute of Science in Bangalore, where he’s been all that time, yeah. He’s been very successful. He’s now a Fellow of the Royal Society and has won several awards in various places. He is one of the inventors of active matter, which is a big thing these days.

Zierler:

Right, right. Now in terms of your self-criticism with graduate students, is that more like your own interests and style or is it more like you don't do the kind of research that’s particularly conducive to serve as a mentor for graduate students?

Lubensky:

You know, I don't really don’t know. I’m not… You know, some people have a personality where they’re out sort of mixing it up with the graduate students all the time. I don't particularly have that personality. Yeah, I don't… One of my smartest students didn't get tenure at UCSD, which kind of upset me a little bit. But I’ve had some surprise post-docs who have succeeded. My most recent is Xiaoming Mao, who has just been promoted to tenure at the University of Michigan, was outstanding. I also had a surprise postdoc Leo Golubovic who came out of the “blue” from Serbia. I learned a great deal from him.

Lubensky:

Yeah, right.

Zierler:

In terms of undergraduate teaching, what were your favorite courses to teach?

Lubensky:

Oh, the one I liked the most was the honors freshman course, teaching mechanics from Kleppner and Kolenkow’s book and E&M from Purcell’s book. Oh, But that’s because of the really bright kids who would do anything you would tell them to do, and so you knew you were teaching them the basics and they were having a lot of fun.

Zierler:

Now were these mostly non-physics majors that you were teaching in this class?

Lubensky:

Oh, no. The honors course was principally physics majors. Yeah. I didn't mind teaching. Some people hated teaching the premeds. I think that was nice. I enjoyed that. I must say that over time it’s become more difficult to teach the undergraduates. They both know more and they know less, and they’re much more uptight about where the world is going to take them. It’s really, really sad to see how much pressure they have on them to succeed.

Zierler:

Yeah. Now more than ever, right?

Lubensky:

Now more than ever, yeah, yeah. It really creates a tension that… It means you're constantly being judged. It’s the professor’s fault if they don't learn, whereas from my background I just described at Caltech, it’s the fault of the student, you know? [Laughs]

Zierler:

Right, right. That’s a generational difference. That probably has less to do with physics.

Lubensky:

Yeah, yeah.

Zierler:

That’s interesting. When you say they know more and less at the same time, I wonder if you're thinking specifically of the Internet.

Lubensky:

No, more what’s happened with the high school education in a sense, you know? Many of the students come in with AP and they really don't know as much as they think they know. The internet does, however, makes life more difficult for the Professors. I worked all of the problems in Kleppner and Kolenkow and made my solutions available to the students after they handed in their homework. Now Googling K&K produces several web pages with all problems solved and presented in clean Latex.

Zierler:

Right.

Lubensky:

That creates tension.

Zierler:

Because an AP physics class is not the same as a college physics class.

Lubensky:

Correct. But the difficult thing with the students you usually have is trying to understand how math works in physics. You know, there’s sort of a divide. They take linear algebra in their math class, and then we go and do harmonic oscillators in physics and it just is difficult for them to see the connections between the two though they really are the same. One of the most shocking things was the fact when I first came to Penn, you could give a final exam in physics and assume that people could solve two equations and two unknowns in the exam. No. They can't do that anymore. So yeah, I basically enjoyed physics. As time went on, teaching became more difficult. My last courses were teaching the sophomore-level course on waves, and actually, there’s a possible book that may come out of it. But I had the point of view that, well, it’s my duty to teach you something that you don't know, and it involved a lot of mathematics and it was not too popular.

Zierler:

Yeah, yeah. So bringing the narrative right up to the present, what kind of projects have you been engaged in in recent years?

Lubensky:

Okay, so here’s one of these cross things. Let me just make sure I get this straight. I just want to remember exactly the details of how it comes. So we hired Andrea Liu from UCLA when I was department chair, and she did a lot of things on jamming. There was… You know, this word universality came up again.

Zierler:

Yeah.

Lubensky:

So the network that forms at the point where you jam things together has a particular character, and it controls what happens nearby. So it’s a little bit like the renormalization group stuff, and they kept saying that, well, you know, when you just balance the number of degrees of freedom at the sites you have with the number of constraints you impose, that’s what creates the state right at the jamming. So they call it isostatic, if you’ve heard that word before.

Zierler:

Yeah.

Lubensky:

Actually, the physicists used it slightly differently from the engineers, I found out, but she was saying that… They and… Actually, de Gennes’ son, Mathieu Wyart, was involved very much in that as well. So I attended Andrea’s group meetings and they said, “Well, you know, you have all these lattices that have exact compensation, i.e., the number of neighbors that are connected to a site is equal to twice the spatial dimension - the number of degrees of freedom of the sites is just balanced by the number of constraints that the bonds give you.” The random configuration of isostatic lattices formed by jamming are isostatic, but there are many periodic lattices that have exact compensation, and I asked myself if they are isostatic, do these lattices have the same properties and the jammed lattices. So there’s a square lattice. There’s a cubic lattice. There’s the kagome lattice. There are all kinds of periodic lattices that have… in two dimensions, four neighbors; in three dimensions, six neighbors. So I started looking at what happens. If you take those lattices and add some extra bonds, that should mimic what happens when you compress the jammed lattice a little bit more. So we got some results that were similar to what they’d gotten in the…but for the wrong reasons in the end, I think. So then we looked at the kagome lattices. So do you know what the kagome lattice is? It and the twisted kagome lattice are depicted in Fig. 9.

Figure 9: Left the kagome lattice. Notice the straight lines of bonds along three directions. Right the twisted kagome lattice obtained by rotating corner sharing triangles in opposite directions. Both are isostatic in that each site has four neighbors. The phonon excitations of the two are quite different, however.

 

Zierler:

No.

Lubensky:

So we studied what happens when next-nearest-neighbor bonds are added to the square, kagome, and cubic lattices and obtained results that were similar to what had been bound near the jamming transition, but partially at least for the wrong reasons.

But then we asked the question, what happens if we take the triangles of the kagome lattice and twisted them? Amazing things happened that totally surprised us. I mean, this is a little bit technical detail, but eventually what it did was it led us to the realization that these lattices share some of the properties that the quantum topological insulators share. So I saw that, namely that… Well, if you go back to the Su-Schrieffer-Heeger model, right, that model… Have you run across that before, the Su-Schrieffer-Heeger model?

Zierler:

No.

Lubensky:

Well, it’s polyacetylene, depicted in Figure 10. Note the alternation of double and single bonds creating a dimerized state. If there were no alteration, your electronic structure would have no energy gap. In other words, the energy as a function of wave number comes in as shown in Fig. 11, left. The dimerized state has a gapped spectrum as shown in Fig. 11 right.

Figure 10: Schematic of the two phases of polyacetylene.  The round dots represent carbon atoms.  The unit cell consists of two carbons, and each carbon is connected to one nearest neighbor carbon with two bonds and to the other with three bonds.  The carbon valence of four is completed with a hydrogen atom connected to each site but not shown.

Figure 11: Left, gapless band structure of undimerized polyacetylene; right gapped spectrum of dimerized polyacetylene.

The phonons of the untwisted kagome lattice has lines of zero modes that become gapped like the electronic states of dimerized polyacetylene with the lattice is twisted. I didn't know much about the arithmetic on how the topological states worked, and I would go in and talk to Charlie Kane and Gene Mele, who invented the topological insulators. I would say, “I think there’s something topological here.” But mostly I got disbelief. Finally, I cornered Charlie one day, and we finally saw that there was, and so we put together a whole theory of topological mechanics that is now quite a popular thing. There are lots of people working on it.

The thing that’s interesting about it is that with the new technologies of additive manufacturing, you can actually make these lattices and measure what goes on. So that was… This is one thing that could possibly have some applications later on because it has the peculiar property—and this has been verified experimentally—that what you have… What the topology says is that I have a mode that’s restricted to be in the neighborhood of an edge. Now if you take a standard sample that’s not isostatic, you have what’s called a Rayleigh wave on free surfaces, so that’s a little bit like the wave in an ocean, only it’s a wave on a solid. It’s important for earthquakes. So what happens in the normal sample is you have a mode here (on one surface) that has a finite frequency and down here (i.e., the opposite surface) a finite frequency, and these two are equivalent. They just depend upon the elasticity. You go to these exotic lattices and you go to the topological ones [Fig. 12]; as you switch from the non-topological lattice to the topological lattice, you move a zero-energy mode on one surface to the opposite one. So whereas you originally have one zero mode per wave number on both the top and the bottom, when you go to the topological one, the top zero mode moves to the bottom. What that does is make the top surface rigid and the bottom surface wiggly, and that has been observed experimentally. So you might imagine some kind of special material that you put in a football helmet or something for which that might be useful. It’s not there yet, but anyhow, that’s what I’ve been spending the last five years on and we’ve gotten a lot of mileage out of that. Yeah.

 

Figure 12: Three distorted kagome lattices: (a) the twisted kagome lattice, (b) transition lattice with zero modes, and (c) topological lattice with asymmetric distribution of zero-frequency edge modes. The insets color code the lowest-frequency modes (dark is lowest frequency).

 

I’m now starting to look at something called odd viscosity, which is a “non-viscous” viscosity that occurs when you have broken time-reversal symmetry. If you have a system that has spinning objects in it, that breaks time reversal, then Onsager says that when you have that, viscosity has a part that’s odd under a change of the spin direction, like changing the magnetic moment from pointing up to pointing down. It also is odd under interchange of the indices of the viscosity, and that means that that viscosity really is non-dissipative and you have non-decaying normal modes associated with it if the normal viscosity is zero. So we’re developing a theory for this that goes back to… Well, one of the more fun things I did years ago with Jerry Gollub is… So do you know what a rattleback is?

Zierler:

No.

Lubensky:

You may know it and you don't know you know it. So if you’ve ever been to a science museum, you have these. They sell these pieces of plastic that look like the hull of a ship. You spin and they spin in one direction…

Zierler:

Oh, yeah! Yeah, yeah!

Lubensky:

…and they stop and spin in the opposite direction.

Zierler:

Yeah.

Lubensky:

You scratch your head. “Why the hell does that happen?” So several years ago—I mean, this is now decades ago, actually—we had a mathematician of Japanese origin who came and talked about rattlebacks. He introduced us to the Russian rattleback, [Fig. 13] which is a perfect symmetric hull with a deck that’s flat. You turn it over and it has an axis of symmetry running parallel to the hull. Then on the deck you have two turtles, one at the bow and one at the stern, which have… You know, if you point the turtles like this (toward each other) and spin it, the thing will spin in both directions. If you point it like this (in opposite directions perpendicular to the symmetry axis), they will spin only with their heads in the direction of the spin. That told us that it was chirality that determined whether or not this would spin, in one direction only, and if you look closely at the rattlebacks you can buy in an American store at a museum, there actually is an asymmetry that’s very subtle to the hull.

Figure 13: Russian rattlebacks

 

So I had the idea that we could shake chiral objects and make a gas out of them. I called Jerry Gollub and asked if he had one of these vibrating tables. He did, and so we got an undergraduate to take a wire, bend it into a C-shape [Fig. 14], and then twist it so that it was no longer planar. We put it on the vibrating table. When the top arm was twisted clockwise, the rattleback would spin in one direction, and when the arm was twisted counter-clockwise, the rattleback would spin in the opposite direction. Then he made the poor undergraduate student make 300 of them, and we put all of them on the vibrating table. The resulting spinning eventually led to a vortex in which the centers of mass of the rattlebacks rotated around the center of the table.

Figure 14: Schematic of the chiral “twisted C’s”

So that idea has come back now in spades. There’s some really beautiful work that’s being done at the University of Chicago by William Irvine where he takes little nanomagnets and then he puts on a rotating magnetic field causing the magnets to spin, and so he has a two-dimensional version of that fluid. It has edge modes that are topologically protected, very much like the things that go on in topological insulators. So that’s why I’m going back to that, and it’s actually taking me back to the original work I did in 1971 on nematic liquid crystals.

Zierler:

Yeah, yeah. So I think, Tom, at this point we’ve come up to the end of the narrative.

Lubensky:

Of the interview?

Zierler:

No, no, no. Not the end of the interview. I want to ask now sort of a few questions that are broadly conceived that you can conceive of your career as a whole. The first one I want to ask--

Lubensky:

Great.

Zierler:

Okay. So my question is looking at your CV, you have a remarkable level of service in physics in terms of external review boards, in terms of editorial boards, and things like that. I want to ask just very generally what… No matter what particular role you're playing as an advisor, as an external reviewer, as somebody who’s providing institutional support, what are some of the main motivating factors that you have in terms of advancing physics, in terms of broadening opportunities, in terms of improving the field that sort of might as a whole serve to inform any kind of advisory or service role that you take on?

Lubensky:

Well, you know, I think everybody in a community like ours has to have some sense of civic duty. I am not the sort of person who really takes a big leadership role to change things, but I do feel it’s important that we do things that serve our community. Some of them are really fun and some are somewhat painful, you know, that you go through all kinds of things. I mean first of all, I want to say that if you look at the CV of almost anybody who’s been around as long as I have, you’ll have the same sort of service record. I don't think mine’s particularly outstanding. There are many people who spend much more time on these things than I do. But it’s important to make sure that we maintain the integrity of our journals and publication, which means that people like me do have to review manuscripts and proposals, serve on editorial boards, and at my stage, review physics departments and the like. Reviewing is really one of the more difficult jobs we have…

Zierler:

Yeah. Yeah.

Lubensky:

…because you know, the world is so intertwined now that everybody is watching out for everyone else to make sure that the papers are cited and… You get letters now from people saying, “Don't forget to cite me,” and so forth. So it’s now--

Zierler:

Everyone’s concerned about their h-index.

Lubensky:

Absolutely, their h-index. Right. [Chuckles] Yeah. That, I think, has really done us a lot of harm. If you look at Phys Rev Letters now, it used to be that you would have three inches of references; now you have whole pages of references to make sure that you get everybody who might be a reviewer.

Zierler:

Right, and I’ve heard it said that one of the problems there is that, perversely or ironically, what the h-index has done is that nobody really reads anyone else anymore. They just cite.

Lubensky:

There’s a lot of that that goes on. That’s been going on for some time because everybody does a better job than their predecessor in formulating the problem. [Laughter] So why do I have to worry about… But you know, in some sense it’s more honest that way. It used to be that you would only reference people…articles that you actually used in writing the paper, not to set the background for the subject. But be that as it may, doing those editorial things are important, and I haven't done as much as many people. I’ve not been an editor of Reviews of Modern Physics or anything like that where you really do take a lot of time and responsibility. I served on the editorial board of PNAS, and that was really difficult because you had to find referees and reviewers, people who know the field well enough to actually be a good guide, whom you know are fair, etc. Often, I would get papers in a field that I just knew nothing about, and it was difficult to do.

Zierler:

Yeah. Yeah. The next question-- Go ahead. No, I’m sorry. Go ahead.

Lubensky:

You know, some of the things… Certainly, I served as… I ran one Gordon Conference. I’ve served on several committees in the National Academy, which I think are important. The last one was a particularly difficult one. The decadal survey was…

Zierler:

Yeah.

Lubensky:

…you know, all of material science and condensed matter physics, basically. So you had lots of clashes of culture. In the end, it was not the product that I had hoped it would be, but it certainly took…you know. I lost some hair, you know. [Chuckles] Yeah. But I did serve as department chair for eight years, and that’s an important job and it’s one that almost everybody, including me, would try to avoid, not without reason, because you're stepping out of the bounds of science into the bounds of sociology and human interactions and all of that. But one of the things I did there was I hired five women, and that’s really been a great help to the department. They really are great people.

Zierler:

And I take it that prior to your tenure… This was what, 2001 you started as chair?

Lubensky:

2001, yeah, just two months before 9/11.

Zierler:

So I take it before your time, there were some diversity issues in the department, at least relative to other departments.

Lubensky:

Well, we had two women at the time – Mirjam Cvitic and Fay Selove and about the time I started hiring the women, Fay passed away. She was around for a long time. So we had one woman, and it wasn’t a healthy environment. So I made hiring women a priority. During my tenure as Chair, we hired five women: a particle experimentalist, Evelyn Thomson and two astronomers, Mariangela Bernardi and Licia Verde, and Andrea Liu and Maria Drndic - two condensed matter physicists, the first a theorist and the second an experimentalist. We now have seven women in a standing faculty of about 40, which isn't what everybody wants it to be, but it’s certainly an improvement of what it was before.

Zierler:

Yeah.

Lubensky:

Let’s see. Is there anything else of note? Yeah, and then of course supporting the liquid crystal community was fairly important, I thought.

Zierler:

Yeah, and that actually gets me to my next question. I want to ask. I mean, it was very clear, when you're recounting your experiences in France in 1970, just how big of a deal liquid crystals was, not just to you personally, but in your recognition of what it meant for the field, right?

Lubensky:

Yeah.

Zierler:

So I wonder if you can telescope that sentiment over the course of your career as a whole, right, in terms of did the vision that you see in terms of the impact of liquid crystals—did that play out more or less how you expected in your subsequent decades in the field? Was it as important? Was it not as important? Did it play out in surprising ways?

Lubensky:

Well, you know, it established… You know, it’s part of the canon now, so to speak, and what was particularly exciting in the ’70s about it was that combining that with the renormalization group, there really was a unity amongst theorists in condensed matter that has now sort of deteriorated because the quantum Hall effect and all of that…

Zierler:

Right.

Lubensky:

…brought the quantum people more towards things that are really exotic properties of quantum mechanics; and the soft direction, because liquid crystals very quickly became part of the polymer world and the surfactant world. You have all of these exotic lamellar phases that become devil’s nightmares, they’re called, plumber’s nightmares—you know, these exotic structures where you have holes in complementary interconnected passageways that spontaneously form. You have all of this stuff on diblock copolymers that form smectic-like phases. The hexatic phase in liquid crystals where you have basically local hexagonal rotational order but not crystalline order. In other words, you rotate the thing by 60 degrees and you get the same structure back…which is what you get in a crystal, but the crystal isn't there. It’s just that. So that language has entered into all kinds of things that people do in surfactants…Langmuir monolayers, order in cells. So there’s a new language that came out of that that I think I certainly did not expect when I started. I should also add that liquid crystals are now an important part of colloid science – for example colloids or nanoparticles in liquid crystal hosts.

Zierler:

Yeah. Yeah. So as a prelude to the bigger question I want to ask, the more narrowly focused one is—and it might be hard to answer. It might be hard to pigeonhole you because you’ve referenced and you have worked in so many different subfields. At the end of the day, what kind of a physicist are you primarily?

Lubensky:

Well, I like to say I’m a condensed matter physicist.

Zierler:

Okay. Okay.

Lubensky:

Many people want to call me a soft condensed matter physicist, and indeed, I spent much of my life doing what’s called soft. In association with the MRSEC I did a lot of things in collaboration with experimentalists which were mixtures of soft and statistical physics. Now some people would like to call me a statistical physicist also, which I am, but really, my goal is no longer solving epsilon expansions and things like that. I really like to find… I like to find ideas that have an application that’s beyond just the single field and so on.

Zierler:

Right, right. So now let’s see how that self-identity or definition works with my next question, which is what do you see—not any one single thing because there’s so much there—but sort of in broad strokes, your primary contributions to condensed matter physics?

Lubensky:

Well, I think it’s the idea of order and conservation laws controlling the long wavelength properties of systems. I think that’s a theme that comes again and again, and for the order, really… We’ve talked about 15 different kinds of order already today. In the end, however, it is perhaps my book with Paul Chaikin that will be most remembered. I see it on book shelves around the world, and I am almost always asked to sign a copy with I visit places.

Zierler:

Right, right! [Laughs]

Lubensky:

And the language that you develop for that is universal in a sense, which is sort of the message of the book that I wrote with Chaikin. It’s a language that you also use in quantum mechanical systems, which people sort of lose sight of, but you have nematic phases of superconductors now, for example.

Zierler:

Yeah. Yeah.

Lubensky:

Things like that. Even though they misuse the language a little bit because the nematic is supposed to have fewer rotational variants and they have it on a substrate that defines particular directions, still it’s inspired.

Zierler:

Right, right. On that line, if you can think again broadly, what are some things either personally or as a representative of your field that are really understood now that were not understood at the beginning of your career?

Lubensky:

Well, I think this whole paradigm of how to look at the symmetry in a system and its conservation laws and extract both the elastic properties and the dynamical properties. That’s… And then, of course, along with it, the language of correlation functions. Yeah. But I guess also you want to, well, in some sense remember that physics has a long history and it goes in phases. People had essentially forgotten about elasticity by the time I started, and now it’s back again in many, many ways, including the topological things I talked about and using elasticity to… For example, this negative viscosity thing—people are talking about having solids now where you have spinners in the middle of it, and what does that do to the dynamics in the system? So you're actually reaching back to… In fact, in the most recent thing I’ve been doing on odd viscosity, we had to go back to Lamb’s classic elasticity book published in 1919. It shows you how to do a proper job of calculating the Rayleigh wave.

Zierler:

Now to--

Lubensky:

And I do like to borrow things from other systems. There’s something called an instanton in particle physics or in field theory, and we use those to calculate certain bound states in percolating systems, for example. The language of physics, I think, is universal and it’s changing now. All of this numerical stuff with machine learning and so forth is really changing the paradigm, and I don't know where that’s going to go relative to where…

Zierler:

For the better, for the worse, or neutral?

Lubensky:

Well, it’s undoubtedly true that some things are being discovered now that you couldn't do otherwise. I think there’s more hype--

Zierler:

And that would assume that it’s worth discovering these things, that it’s not just…

Lubensky:

Yeah. Yeah. Well, you know, people, material scientists now will tell you, “I know how to do density functional theory so well now. You give me the set of properties that I want from the solid and I’ll run my AI and deep learning thing and I’ll come up with the best compound that will give you all those properties.” That’s something you couldn’t do otherwise. On the other hand, it’s numerics and it’s really hard sometimes to understand why the answer came out that came out.

Zierler:

Right, right. And where is imagination and creativity in that?

Lubensky:

Where is imagination and creativity—yeah, yeah.

Zierler:

Right, right. So to flip that question on its head, what in your field remains poorly understood or mysterious now that might even be surprising at this point? Maybe we should have a better handle on this.

Lubensky:

Hmm, hmm. Well, what people want to know in the material science community, which is really a lot of the condensed matter, is just how you can make things, how you can control the fabrication of material to have the properties you want. So that’s… And there are a lot of physicists who look at that, and it’s certainly very important for our economy and so forth. I think we’re going to see more of that going along.

Now there are the… The quantum condensed matter people have all of these exotic new phases that have quasiparticles that have exotic properties and so forth. In fact, that’s a fairly vibrant field that I think we’re going to see more and more of, and maybe you’ll see something in quantum computing that comes out of it. But that certainly is the center of much of the condensed matter work that’s going on now is the quantum computing stuff—you know, exotic properties of quantum things at a distance.

Magnetics and how to control all microscopic magnetic properties is coming back. Then you have these surprising things like the twist phases of graphene and so forth. You twist it by 1.7° and you get a new topological insulator, things like that.

So I think that we will see a lot of growth in the area of new materials presenting new questions, which has been true for a long time. There are questions in things like mathematical topology and so forth we don't fully understand—you know, the whole business of how do you obtain a full description of the defect properties of layered structures? It’s a very profound mathematical problem that we don't fully understand, and there are others like that around.

In soft matter, I think it’s mostly… What’s going to set the stage for growth is finding better ways of fabricating materials and synthesizing them. There are improved methods of looking at things down at the micron scale and so forth.

The other big questions, of course, that a lot of people are interested in are active matter in all of its forms. That’s going to be something where… We certainly don't have control over that yet. It’s very appealing because there are just myriads of numerical experiments you can do, so a lot of people jump in and do that. It certainly is increasing our understanding. But that then gets… Its interface with biology is certainly a big question. So there’s been a change in the posing of biological problems recently that for a long time mechanics was not considered an important part of the whole biology realm, and now there’s always some kind of chemical/mechanical interaction that is responsible for growth and so forth, and we’re just beginning to get a hold of that.

Zierler:

Right, right.

Lubensky:

That’s…yeah.

Zierler:

So I think, Tom, for my last question, it’s a forward-looking question, rhetorical to some degree, and that is… I mean, you’ve already touched on a lot of the things that are exciting potentially for the future, both in a theoretical and an applied sense, but I wonder if there is the proverbial graduate student who is looking to start a career in condensed matter physics and they have 40 or 50 years ahead of them in their career. What kind of advice would you give in terms of the kinds of topics to focus on, the kinds of technologies to pay attention to, the kinds of people to collaborate with? What might be, for this proverbial graduate student, the kinds of advice you would give him or her?

Lubensky:

So it’s always not a particularly good idea to have a septuagenarian giving advice to a 20-year-old. [Laughter]

Zierler:

No, but see, as a historian—no. As a historian, right, the value in your experience is the power of extrapolation, right?

Lubensky:

Right. So I would give some advice to graduate students that is hard for them to take right now, and that is don't forget to learn the fundamentals.

Zierler:

And you think that’s unique to this generation? You would never have needed to been told that?

Lubensky:

Well, it’s been developing for a long time. So the model that I grew up under (and most of my mentors) was one where you went to graduate school and you proved yourself with some kind of exam, you know, candidacy exam that you know the core.

Zierler:

Yeah. You mean no matter what your specialty is, you know the fundamentals.

Lubensky:

Right, yeah. What’s broken that image, the dream that there is a common core in physics, is basically money, and that has to--

Zierler:

So that’s to say there really is no more common core in physics?

Lubensky:

Very difficult.

Zierler:

Wow.

Lubensky:

You know, it used to be that in my time. There were two years of courses, including mechanics, electrodynamics, quantum mechanics, statistical physics at a minimum and a smattering of more specialized courses: solid-state, high-energy and nuclear physics, field theory, and maybe mathematical physics. For the most part, people did not start their research until after that was over. I certainly didn't start. Now there are many more options: biological physics, liquid crystals, polymers, astronomy, cosmology, and so on. You can argue that accelerator scientists do not have to take condensed-matter physics and vice versa. And maybe now trying to create the “well-rounded physicists” is unrealistic and maybe a waste of time. there is also the problem that the current funding model makes students, particularly experimental ones, both a student and an employee, right? So the focus is on getting the experiment done, and in my mind, that’s not the best way to make a career because you never know from what little corner of the world you're going to find something that’s going to help you out, right?

Zierler:

Yeah, yeah.

Lubensky:

It’s like what they tell people today, that your career is not going to be a single-subject career, for the most part. You want to be able to… There’s some flow through stages, which means you need to know a lot, and unfortunately the students, really in a sense, have to know more than we do. They have to know computers now.

Zierler:

Right!

Lubensky:

And that is a major undertaking in my view. There are so many easy ways of wasting time at the computer.

Zierler:

Yeah, yeah, and the danger is that they can know the computers without knowing the fundamentals, and then what’s the value of their partnership with the computers?

Lubensky:

Right, right. And that certainly is more common now. You can't… Contour integrals and that kind of stuff are things that students just don't do. They avoid it if they can, whereas I always took it as a challenge. You know, can I figure out how to do this? Now has that been helpful to me? Maybe not. Maybe I should have gone into more computers now because it’s certainly where the world is. So students and post-docs that I have a little bit of a disadvantage that they don't get into the midst of things, because there’s no doubt that computers are going to become even more and more important. You're going to see more and more machine learning and AI and all of that directing, finding out things and hidden truths about… Now of course that means there’s a tendency to go after problems that are complicated that you couldn't go after before.

Zierler:

And then there’s the question, even if you find these answers, what do you make of them if you don't have the fundamentals?

Lubensky:

Right. Students should also have an open attitude towards the other sciences and not… More and more you can argue, “Well, you should take some biology because you might end up with that,” or maybe, you know, “Don't be afraid of looking at materials science.” There are more likely to be jobs there than there are in physics.

On the other hand, for physics itself, we are in exciting times of pure fundamental physics. I mean the whole business of the cosmology and dark matter and black holes and super galaxies and accelerating expansion of the universe … You know, all of those things and what they’re doing largely because of the data and clever ways of imaging the world or the universe—we’re really learning a lot and faced with the biggest unknown of all, two of them: what are dark energy and dark matter? Who knows? So if you're really inspired by the fundamentals of physics, that’s where you want to go, right?

Zierler:

Yeah, yeah. Well, Tom, it has been an absolute pleasure talking with you today. I really appreciate your time.

Lubensky:

Well, good. I’m happy to share my history and past. I should close with one thing.

Zierler:

Please.

Lubensky:

One of the things that the liquid crystals did was to sort of encourage the growth or encourage the use of what we call mass density waves to describe order, and that was really important for our understanding of quasicrystals, for example, which you would not have thought. So there was the quasicrystal sort of set up. It’s much easier to do arithmetic with waves with fivefold symmetry than it is to figure out where the atoms go.

Zierler:

Right, right. Well, great. Okay, Tom, I’m going to cut the recording here.

Lubensky:

Okay, good. I enjoyed it.